巴戦を状態遷移図で解いてみよう

大相撲どすこい研という番組で巴戦の話があったので、久しぶりに「巴戦って平等じゃないんだっけ？」という確認がてら、計算してみました。

まあ、情報工学科をちゃんと卒業したので、情報系らしく状態遷移図を使って証明してゆきたいと思います。

今回使ったもの

• 紙とペン
• PowerPoint
• Python3（こんなのはなくても証明できます）

たくさん実験してみる

ここはPythonを使ってしました！

力士はA、B、Cの3人。最初に戦うのはA、Bの2人。

力士の強さはみんな平等だとします。つまり、どの力士も勝率50%です。

C言語で書けばもっと高速に実験ができると思います。やってみてください（手抜きをここでする）

from random import choice

count = 100_000

wrestlers_str = 'ABC'
wrestlers = set(wrestlers_str)
need_win_count = len(wrestlers) - 1
won_count_dic = {wrestler: 0 for wrestler in wrestlers}

for _ in range(count):
    #print('=' * 32)
    _win = 'X'
    win = 'X'
    dohyo = set(wrestlers_str[:2])
    win_count = 0
    while True:
        _win = choice(list(dohyo))
        #print(dohyo, _win, win)
        if win == _win:
            win_count += 1

        if need_win_count == win_count:
            won_count_dic[win] += 1
            break

        win = _win

        dohyo = {_win, choice(list(wrestlers - dohyo))}

print({wrestler: won_count_dic[wrestler]  / count for wrestler in wrestlers_str})

んで、結果はこんな感じです。

{'A': 0.35702, 'B': 0.35574, 'C': 0.28724}

あれれ〜？

なんか最初に戦わないCだけが弱いぞ〜？🤔

Cを見るとなんだか2/7くらいの値になっていますね。

状態遷移図で解く

というわけで、状態遷移図で解いてみましょう。

数学的に解くのは無理（ではないがポテトサラダを作るくらい面倒）なので、省きます。

状態遷移図の説明は省きます。このページに来た人は、たぶん、状態遷移図を知っていると思うので。

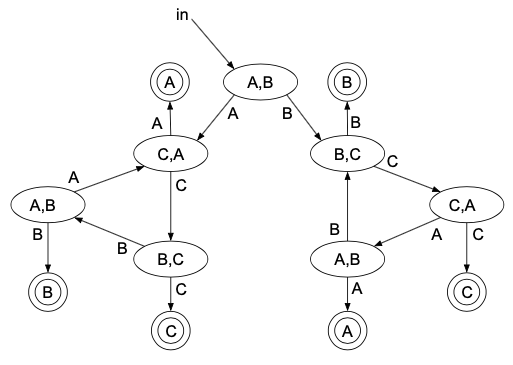
では、状態遷移図を書いてみましょう。

こう書ければ正解です。

一方で、よくある間違いがこれです。

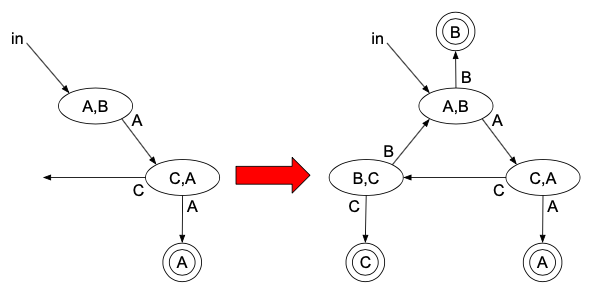
このように書いてしまうと、最初にBが勝ったら終わってしまうので、ダメです。

では、ちゃんとした方の状態遷移図を使って、計算してみましょう。

ちなみに、in→A,B以外の遷移する確率は全て\( \dfrac{1}{2} \)とします。

まず、Aが優勝する場合について考えます。まず考えられるのは「Aが2連勝する」場合。

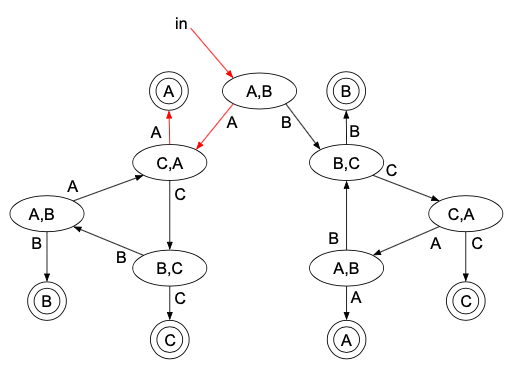
このようになる確率は\(\dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{1}{2^2}\)ですね。

次に、「A,C,B,A,Aの順で勝つ」ことでAが優勝する場合は、このような遷移をたどることになります。

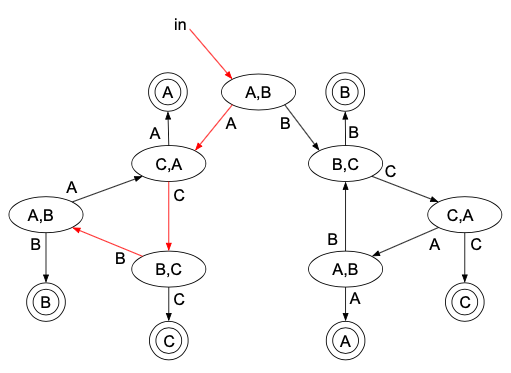
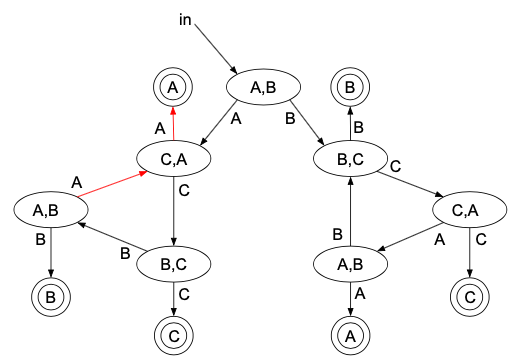
矢印をたどってみると、このように勝つ確率は\(\dfrac{1}{2^5}\)だとわかります。

また、ここから「A,「C,B,Aをn回繰り返す」,Aの順で勝つ」が\(\dfrac{1}{2^{3n+2}}\)と、なんとなくわかります（本当は数学的帰納法とかいうやつをしないといけないけど、割愛）

次に、「B,C,A,Aの順で勝つ」場合を考えます。

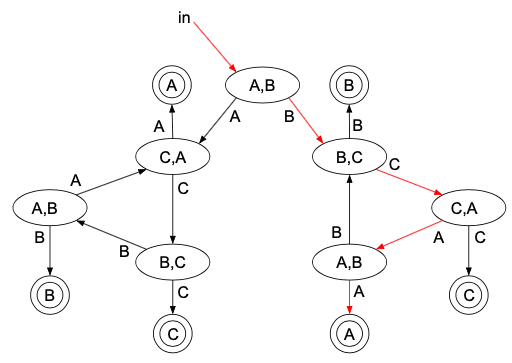
この結果は\(\dfrac{1}{2^4}\)です。

また、「B,C,A,B,C,A,Aの順で勝つ」の場合は、このようになります。

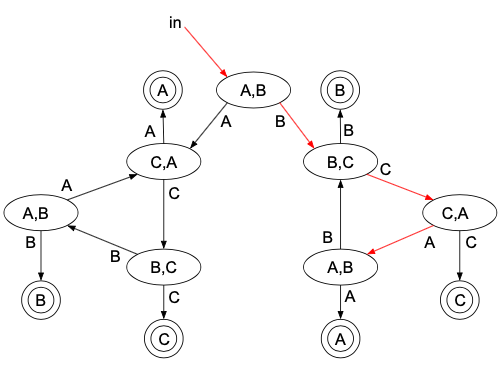
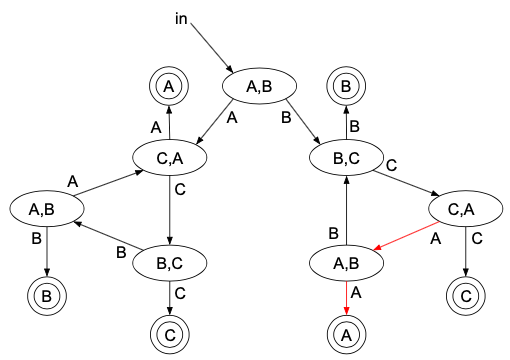
この結果は\(\dfrac{1}{2^7}\)です。

このことから、「B,「C,A,Bをn回繰り返す」,A,Aの順で勝つ」が\(\dfrac{1}{2^{3n+4}}\)と、なんとなくわかります。

つまり、Aが巴戦で勝つ確率は\(\displaystyle P(A)=\sum_{k=0}^n \left(\frac{1}{2^{3k+2}}+\frac{1}{2^{3k+4}}\right)\)となります。

次にBが優勝する確率を考えよう、と思いましたが、Aと同様に考えれば良いので、Bが巴戦で勝つ確率も\(\displaystyle P(B)=\sum_{k=0}^n \left(\frac{1}{2^{3k+2}}+\frac{1}{2^{3k+4}}\right)\)となります。

さいごに、Cが確率について考えます。まあ、余事象なので\(P(C)=1-P(A)-P(B)\)で求められますが、それではあまりにも無慈悲なので、Cについてはちゃんと遷移図で考えましょう。

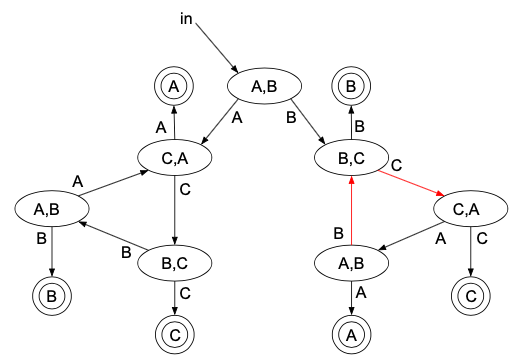
まず、「B,C,Cの順で勝つ」場合を考えます。

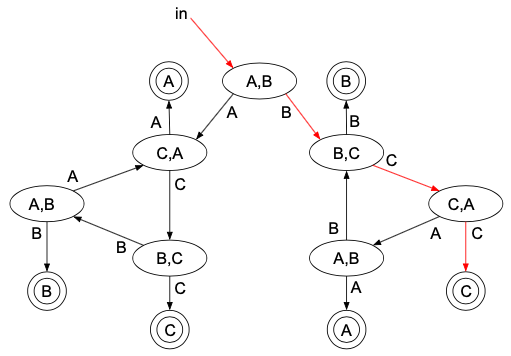
結果は\(\dfrac{1}{2^3}\)です。

次に、「B,C,A,B,C,Cの順で勝つ」場合は、

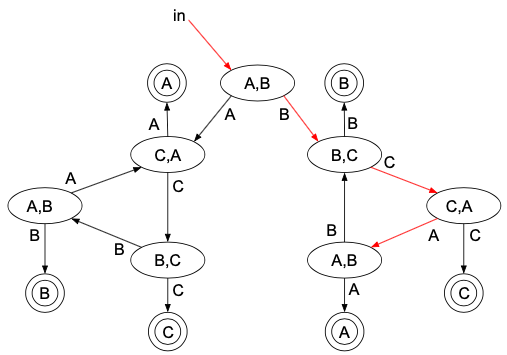
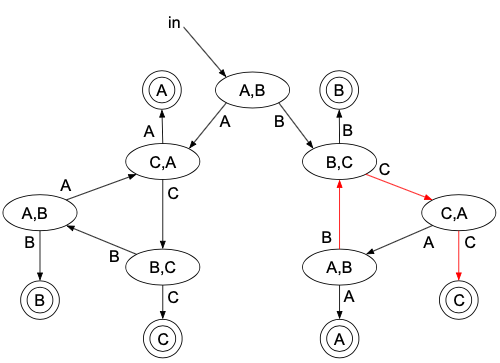
\(\dfrac{1}{2^6}\)となります。

このことから、「B,「C,A,Bをn回繰り返す」,C,Cの順で勝つ」が\(\dfrac{1}{2^{3n+3}}\)と、なんとなくわかります。

また、Aが最初に勝つ場合も同様だと考えられるため、Cが優勝する確率は、\(\displaystyle P(C)=2\sum_{k=0}^n \frac{1}{2^{3k+3}}\)となります。

さいごに\(n\to\infty\)とすると、

\(P(A)=P(B)=\dfrac{5}{14}, P(C)=\dfrac{2}{7}\)

おお！　確かにCが2/7になったね。

さらなる考察

プログラムのwrestlers_str = 'ABC'をwrestlers_str = 'ABCD'とすると、4人の巴戦の結果が実験的にわかります。プログラムを動かしてみてね！🤗🤗（完全に手を抜いている）

さいごに

これを解いたときに、「そういえば状態遷移図で巴戦を解くって、なんとなくやったことあるな？」と思ったのですが、おそらく、大学時代に解いたんだと思います。