マルコフ連鎖で明後日の調子を予測する

学部3年のとき、シミュレーション論という講義で、マルコフ過程により次の状態、さらにその次の状態を予測するということを行ないました。

これをプログラムで実現します。

マルコフ過程とは

ある時点における現象の確率が直前の結果だけで決まる確率過程をマルコフ過程と言います。

特に離散時間 \( \{t=0,1,2,…\} \) や離散値 \( \{i; i=0,1,2,…\} \) を取るものをマルコフ連鎖と言います。

と言われてもよくわからないので、図で説明します。

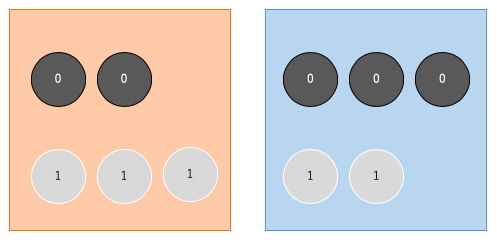
まず赤と青、二つのボックスを用意します。その中にはそれぞれ黒玉2白玉3、黒玉3白玉2を入れます。

次に、それぞれのボックスから玉を1つずつ取り出し、交換してそれぞれのボックスに玉を入れます。下の画像は、赤のボックスから白玉を、青のボックスから黒玉を取り出し、それを交換したものです。

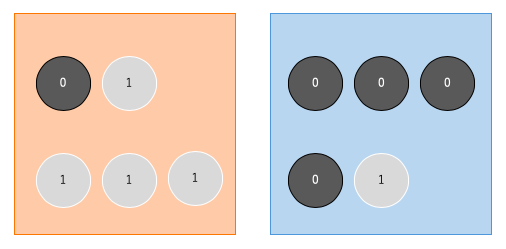
この作業を繰り返します。

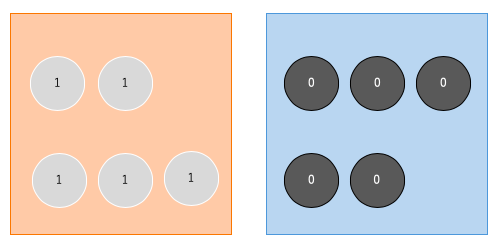
この作業をすると、最初は\( (t = 0) \)赤から黒玉を取り出す確率が\(2/5\)だったのに対し、次の状態では\( (t = 1) \)その確率が\(1/5\)になっていることがわかります。

このように、ある時点の確率は1つ前のプロセスに依存していることがわかります。

本題

例えばこのような問題が出たとします。

ある機械の調子は、0: 良い、1: 普通、2: 悪いの状態を毎日次の推移行列のマルコフ連鎖で推移する。今日の調子は悪かった。明後日の調子を予測せよ。

$$ P = \begin{bmatrix} 0.5 & 0.4 & 0.1 \\ 0.3 & 0.4 & 0.3 \\ 0.2 & 0.3 & 0.5 \end{bmatrix} $$

さて、どのように解くか。

とりあえずプログラムを書きます。

import numpy as np


class Solver(object):

    def __init__(self, P: np.ndarray, cond_li: [str], current: int):

        rows, cols = P.shape
        eps = 1e-8
        # 推移行列は正方行列でなければならない。
        if rows != cols:
            raise Exception(f'P must be square. <{(rows, cols)=}>')
        elif rows - 1 < current:
            raise Exception(f'must be rows - 1 >= current. <{(rows, current)=}>')
        elif np.any(np.abs(P.sum(axis=1) - 1) > eps):    # == にできないのは、誤差的な問題
            raise Exception(f'P.sum(axis=1) must be 1. <{P.sum(axis=1)=}>')

        self.P, self.cond_li = P, cond_li
        self.α = α = np.zeros(rows)
        α[current] = 1


    def get_result(self) -> {str: str, str: float}:

        α, P = self.α, self.P
        # 明後日の結果を予測する。
        mat = α @ P @ P

        return {'状態': self.cond_li[np.argmax(mat)], '確率': np.max(mat)}



if __name__ == '__main__':

    P = np.array([[.5,.4,.1],
                  [.3,.4,.3],
                  [.2,.3,.5]])
    cond_li = ['良い', '普通', '悪い']
    current = 2

    svr = Solver(P, cond_li, current)
    print(f'result: {svr.get_result()}')

ここで、\(\alpha\)を現在の状態を表すベクトル（例えば、状態が悪ければ\(\alpha=(0,0,1)^T\)となる）、\( P \)を推移行列としています。

ちなみにベクトルや行列の掛け算をNumPyで書くとき、最近では np.dot(A, B)以外にもA @ Bが使えます、便利。

ちょっと面倒なのは\( P^2 \)をP ** 2ではなくP @ Pと書く必要があるところです。SciPyならそれで書けるのにね。

「今日体調が悪かった、じゃあ明日は？」なら\( \alpha P \)、「明後日は？」なら\( \alpha P^2 \)で求まります。

結果は？

result: {'状態': '悪い', '確率': 0.36}

どうやら36%の確率で明後日も体調が悪いようです……。

さいごに

学部講義のシミュレーション論では実際にプログラムを組むという演習はありませんでしたが、私は「とりあえず組んでみたい！」という一心で組みました。

他にもいろいろプログラムを組んだので、また後ほどアップロードします。

ではまた！

蛇足

数式が使えるようになった！（歓喜）