吸収マルコフ連鎖をプログラムに落とし込む

前回に引き続き、シミュレーション論の復習がてらプログラムを組んでゆきます。

吸収マルコフ連鎖とは

状態が一時的もしくは吸収的な状態からなるマルコフ連鎖のことを指します。

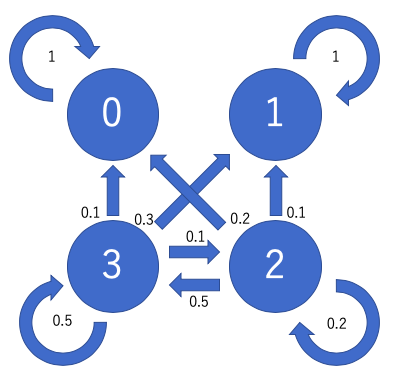
例えば、推移行列が以下のとき、推移図は以下のように表されます。

$$ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0.2 & 0.1 & 0.2 & 0.5 \\ 0.1 & 0.3 & 0.1 & 0.5 \end{bmatrix} $$

推移図を見ると、0、1の状態になるとそこから抜けることができなくなっていることがわかります。これを吸収的なノードと言います。逆に、2、3は一時的なノードと言います。

次に、吸収的なノードから吸収的なノードへ向かう推移行列を\(I\)（単位正方行列）、吸収的から一時的を\(O\)（零行列）、一時的から吸収的を\(R\)（任意の行列）、一時的から一時的を\(Q\)（任意の正方行列）を用いて、\(P\)を以下のようにして表します。

$$ P = \begin{bmatrix} I & O \\ R & Q \end{bmatrix} $$

行列の性質から、

$$ P^n = \begin{bmatrix} I & O \\ (I-Q^n)(I-Q)^{-1}R & Q^n \end{bmatrix} $$

また、極限を取って

$$ \displaystyle \lim_{ n \to \infty } Q^n = O $$

となることから、

$$ P^\infty = \begin{bmatrix} I & O \\ MR & O \end{bmatrix} $$

このとき\(M = (I-Q)^{-1}\)を基本行列といい、\(MR\)を吸収行列と言います。

とりあえず、例題を見てみましょう。

例題

状態空間(S={0,1,2,3})上のマルコフ連鎖について考える。推移行列が上の\(P\)で与えられるとき、一時状態\(j\)から吸収状態になるまでにかかる平均時間と、一時状態\(j\)から状態\(1\)に達する確率を求めよ。

これ、実際に解くとなると、以下のように数式が並びます。

上記のように\(P, I, O, R, Q, M\)を置くと、以下のようになる。

$$ P = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0.2 & 0.1 & 0.2 & 0.5 \\ 0.1 & 0.3 & 0.1 & 0.5 \end{bmatrix} $$

$$ I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $$

$$ O = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} $$

$$ R = \begin{bmatrix} 0.2 & 0.1 \\ 0.1 & 0.3 \end{bmatrix} $$

$$ Q = \begin{bmatrix} 0.2 & 0.5 \\ 0.1 & 0.5 \end{bmatrix} $$

$$ M = (I-Q)^{-1} = \begin{bmatrix} 10/7 & 10/7 \\ 2/7 & 16/7 \end{bmatrix} $$

ゆえに、一時状態2から吸収状態になるまでにかかる平均時間は

$$ m_2 = m_{20}+m_{21} = 20/7 $$

同様に一時状態3の場合は、

$$ m_3 = m_{30}+m_{31} = 18/7 $$

また、

$$ MR = \begin{bmatrix}3/7 & 4/7 \\ 2/7 & 5/7 \end{bmatrix}$$

より、

一時状態2から吸収状態1へ向かう確率は、\( 4/7 \)、同様に一畳状態3の場合は\( 5/7 \)

（解答終）

これは面倒だし、手計算の場合はミスも起きることがあるので、プログラムで組むことにします。

import numpy as np
from pprint import pp as _pp
# 見やすくするために、 pp を改良
pp = lambda *args, **kwargs: _pp(width=-1, *args, **kwargs)


class Solver(object):

    def __init__(self, _P: np.ndarray):

        eps = 1e-8
        rows, cols = _P.shape
        if rows != cols:
            raise Exception(f'_P must be rows == cols. <{(rows, cols)=}>')
        elif np.any(np.abs(_P.sum(axis=1)-1) >= eps):
            raise Exception(f'_P.sum(axis=1) must equal 1. <{_P.sum(axis=1)=}>')
        elif not 1 in _P:
            raise Exception(f'_P must content of 1.')

        self.size = rows
        self._P = _P
        self.setPIORQ()


    def setPIORQ(self):

        _P = self._P

        # _P の基本変形、これをすることによって、標準形に持ってゆく
        self.ix_li = ix_li = np.where(np.diag(_P) == 1)[0].tolist()
        self.Isize = Isize = len(ix_li)
        ix_li += [i for i in range(self.size) if i not in ix_li]
        self.S = S = np.zeros_like(_P)
        for i, ix in enumerate(ix_li):
            S[ix, i] = 1

        self.P = P = S.T @ _P @ S

        #[[I O]
        # [R Q]] の形式に切り出し
        self.I = P[:Isize, :Isize]
        self.O = P[:Isize, Isize:]
        self.R = P[Isize:, :Isize]
        self.Q = P[Isize:, Isize:]


    def mean_time(self) -> {str: float}:

        self.M = np.linalg.inv(np.eye(*self.Q.shape) - self.Q)

        Msum = self.M.sum(axis=1)

        return {f'm{self.ix_li[i+self.Isize]}': Msum[i] for i in range(len(Msum))}


    def approaching_probability(self, cond: int) -> np.ndarray:

        MR = self.M @ self.R
        Omr = np.zeros([MR.shape[0], self.O.shape[1]])
        self.Pinf = Pinf = np.vstack([np.hstack([self.I, self.O]),
                                      np.hstack([    MR,    Omr])])

        S = self.S
        self._Pinf = _Pinf = S @ Pinf @ S.T

        return {f'p∞{(i, cond)}': _Pinf[i, cond] for i in range(self.size)}



if __name__ == '__main__':

    P = np.array([[1 ,0 ,0 ,0 ],
                  [0 ,1 ,0 ,0 ],
                  [.2,.1,.2,.5],
                  [.1,.3,.1,.5]])
    cond = 1

    svr = Solver(P)

    print('一時状態から吸収状態に達するまでの平均時間:')
    pp(svr.mean_time())

    print(f'状態{cond=}に達する確率:')
    pp(svr.approaching_probability(cond))

これによって、出力はこのようになります。

一時状態から吸収状態に達するまでの平均時間:
{'m2': 2.8571428571428568,
 'm3': 2.571428571428571}
状態cond=1に達する確率:
{'p∞(0, 1)': 0.0,
 'p∞(1, 1)': 1.0,
 'p∞(2, 1)': 0.5714285714285714,
 'p∞(3, 1)': 0.7142857142857142}

ちゃんと解けてる！

ちなみに、以下のようなNumPy配列でもちゃんと結果が出力できるように、基本変形で標準形に落とし込んでから計算できるようにプログラムを組んでいます。

if __name__ == '__main__':

    P = np.array([[1 ,0 ,0 ,0 ],
                  [.2,.1,.3,.4],
                  [0 ,.5,0 ,.5],
                  [0 ,0 ,0 ,1 ]])
    cond = 0

一時状態から吸収状態に達するまでの平均時間:
{'m1': 1.7333333333333334,
 'm2': 1.8666666666666667}
状態cond=0に達する確率:
{'p∞(0, 0)': 1.0,
 'p∞(1, 0)': 0.26666666666666666,
 'p∞(2, 0)': 0.13333333333333333,
 'p∞(3, 0)': 0.0}

さいごに

今回は吸収マルコフ連鎖についてプログラムで組んでみました。

思いの外時間がかかってしまいましたが、こうやって書いてみると、計算の仕組みが詳しく理解できました。

ライフゲームを実装するまで、シミュレーション論についてまとめたいなあ、と思いました。