ほぼゼロからニューロンモデルのプログラムを作る

理論については軽く触れるだけにします。今回のメインはプログラムをほぼゼロから組み立てることにあります。

ニューラルネットワークとは？

脳内のニューロンの繋がりをモデル化したものを言います。

これにはニューロセルというものが用いられますが、有名なのはMcCulloch-Pittsニューロンモデルといい、このような図形で表されます。

ここでいうxは入力、wは重み、vは閾値、zは出力を意味します。

ここで、uを以下のように定義します：

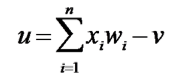
これを出力関数に入れ、zを出力します。

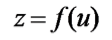
出力関数はステップ関数だったり、シグモイド関数だったりします。

学習規則

学習規則は以下のようにします。

• 入力に対して正解を出力した場合は何もしない
• 入力に対して不正解を出力した場合は以下に従う
  • タイプ1エラー（0と出力すべき入力に1を出力）の場合、結合加重が大きいか、閾値が小さいと考え、結合加重を −1、閾値を+1する
  • タイプ2エラー（1と出力すべき入力に0を出力）の場合、結合加重が小さいか、閾値が大きいと考え、結合加重を +1、閾値を-1する
• 学習する問題に全て正解するまで以上を繰り返す

プログラムを作る

学習器自体はこのように書きました。

def train(x_li_li: [int], _w_li: [int], v: int, ideal_li: [int]) -> [[int], int]:

    w_li = _w_li.copy()
    print(f'{x_li_li =}')
    print(f'{w_li    =}')
    print(f'{v       =}')
    print(f'{ideal_li=}')

    frog = 0
    data_len = len(x_li_li)
    w_li_len = len(w_li)

    for i in range(w_li_len):
        print(f'\tx{i+1}', end='')

    for i in range(w_li_len):
        print(f'\tw{i+1}', end='')

    print('\tv\tz\tideal\texam')

    while frog != 4:
        for i in range(data_len):
            z = 1 if sum([x_li_li[i][j] * w_li[j] for j in range(w_li_len)]) - v >= 0 else 0
            ideal = ideal_li[i]
            if z == ideal:
                exam =  '正解'
            elif ideal == 0:
                exam = 'タイプ1エラー'
            elif ideal == 1:
                exam = 'タイプ2エラー'




            print('\t' + '\t'.join(map(str, x_li_li[i])) + '\t' + '\t'.join(map(str, w_li)) + f'\t{v}\t{z}\t{ideal}\t{exam}')
            if z == ideal:
                frog += 1
                if frog == data_len:
                    return w_li, v
            else:
                frog = 0
                if ideal == 0:
                    v += 1
                    for j in range(w_li_len):
                        if x_li_li[i][j] == 1:
                            w_li[j] -= 1
                else:
                    v -= 1
                    for j in range(w_li_len):
                        if x_li_li[i][j] == 1:
                            w_li[j] += 1

これがちゃんと出力されるのか、確認してゆきましょう。

論理積

プログラムはこんな感じ。

if __name__ == '__main__':

    bit_len = 2
    x_li_li = [[int(i) for i in list(format(x, f'0{bit_len}b'))] for x in range(2 ** bit_len)]
    w_li = [3, 2]
    v = 1
    ideal_li = [eval('&'.join(map(str, x_li))) for x_li in x_li_li]
    train(x_li_li, w_li, v, ideal_li)

出力はこのようになります。

x_li_li =[[0, 0], [0, 1], [1, 0], [1, 1]]
w_li    =[3, 2]
v       =1
ideal_li=[0, 0, 0, 1]
 x1 x2 w1 w2  v  z  ideal  exam
  0  0  3  2  1  0  0      正解
  0  1  3  2  1  1  0      タイプ1エラー
  1  0  3  1  2  1  0      タイプ1エラー
  1  1  2  1  3  1  1      正解
  0  0  2  1  3  0  0      正解
  0  1  2  1  3  0  0      正解
  1  0  2  1  3  0  0      正解

ちゃんと正しく学習できているようです。

論理和

プログラムはこんな感じ

if __name__ == '__main__':

    bit_len = 2
    x_li_li = [[int(i) for i in list(format(x, f'0{bit_len}b'))] for x in range(2 ** bit_len)]
    w_li = [7, 4]
    v = 11
    ideal_li = [eval('|'.join(map(str, x_li))) for x_li in x_li_li]
    train(x_li_li, w_li, v, ideal_li)

出力はこうなります。

x_li_li =[[0, 0], [0, 1], [1, 0], [1, 1]]
w_li    =[7, 4]
v       =11
ideal_li=[0, 1, 1, 1]
 x1 x2 w1 w2  v  z  ideal  exam
  0  0  7  4 11  0  0      正解
  0  1  7  4 11  0  1      タイプ2エラー
  1  0  7  5 10  0  1      タイプ2エラー
  1  1  8  5  9  1  1      正解
  0  0  8  5  9  0  0      正解
  0  1  8  5  9  0  1      タイプ2エラー
  1  0  8  6  8  1  1      正解
  1  1  8  6  8  1  1      正解
  0  0  8  6  8  0  0      正解
  0  1  8  6  8  0  1      タイプ2エラー
  1  0  8  7  7  1  1      正解
  1  1  8  7  7  1  1      正解
  0  0  8  7  7  0  0      正解
  0  1  8  7  7  1  1      正解

こっちもちゃんと合ってる。

任意の問題

例えばこのような問題があるとします。

私は明日、遠足にゆくことになり、お菓子を買うことにしました。310円と220円と70円 のお菓子が商品棚には並んでいます。遠足にこれらのお菓子を買おうとしましたが、持っているお金は500円しかありませんでした。私はどのような組み合わせなら買うことができるでしょう？

プログラムが組めれば、こんな問題だってニューロンモデルで解くことができるようになります。

def test(x_li_li: [int], _w_li: [int], v: int):

    w_li = _w_li.copy()
    print(f'{x_li_li =}')
    print(f'{w_li    =}')
    print(f'{v       =}')

    data_len = len(x_li_li)
    w_li_len = len(w_li)

    for i in range(w_li_len):
        print(f'\tx{i+1}', end='')

    for i in range(w_li_len):
        print(f'\tw{i+1}', end='')

    print('\tv\tz')

    for i in range(data_len):
        z = 1 if sum([x_li_li[i][j] * w_li[j] for j in range(w_li_len)]) - v >= 0 else 0
        print('\t' + '\t'.join(map(str, x_li_li[i])) + '\t' + '\t'.join(map(str, w_li)) + f'\t{v}\t{z}')


if __name__ == '__main__':

    print('TRAIN')
    cost_li = [330, 220, 70]
    x_li_li = [
        [1, 1, 1],
        [1, 1, 0],
        [1, 0, 1],
        [1, 0, 0],
        [0, 1, 1]
    ]
    w_li = [7, 4, 11]
    v = 12
    ideal_li = []
    for x_li in x_li_li:
        tot = 0
        for cost, x in zip(cost_li, x_li):
            tot += cost * x
        ideal_li.append(0 if tot <= 500 else 1)

    # 1は買えないことを意味し、0は買えることを意味する
    train_w_li, train_v = train(x_li_li, w_li, v, ideal_li)

    print('TEST')
    x_li_li = [
        [0, 1, 0],
        [0, 0, 1],
        [0, 0, 0]
    ]
    test(x_li_li, w_li, v)

トレインで5つの教師データについて学習させ、テストでは学習させていない3つのデータを学習させます。

学習の過程はこのようになっています。

TRAIN
x_li_li =[[1, 1, 1], [1, 1, 0], [1, 0, 1], [1, 0, 0], [0, 1, 1]]
w_li    =[7, 4, 11]
v       =12
ideal_li=[1, 1, 0, 0, 0]
 x1 x2 x3 w1 w2 w3   v  z  ideal  exam
  1  1  1  7  4 11  12  1  1      正解
  1  1  0  7  4 11  12  0  1      タイプ2エラー
  1  0  1  8  5 11  11  1  0      タイプ1エラー
  1  0  0  7  5 10  12  0  0      正解
  0  1  1  7  5 10  12  1  0      タイプ1エラー
  1  1  1  7  4  9  13  1  1      正解
  1  1  0  7  4  9  13  0  1      タイプ2エラー
  1  0  1  8  5  9  12  1  0      タイプ1エラー
  1  0  0  7  5  8  13  0  0      正解
  0  1  1  7  5  8  13  1  0      タイプ1エラー
  1  1  1  7  4  7  14  1  1      正解
  1  1  0  7  4  7  14  0  1      タイプ2エラー
  1  0  1  8  5  7  13  1  0      タイプ1エラー
  1  0  0  7  5  6  14  0  0      正解
  0  1  1  7  5  6  14  0  0      正解
  1  1  1  7  5  6  14  1  1      正解
  1  1  0  7  5  6  14  0  1      タイプ2エラー
  1  0  1  8  6  6  13  1  0      タイプ1エラー
  1  0  0  7  6  5  14  0  0      正解
  0  1  1  7  6  5  14  0  0      正解
  1  1  1  7  6  5  14  1  1      正解
  1  1  0  7  6  5  14  0  1      タイプ2エラー
  1  0  1  8  7  5  13  1  0      タイプ1エラー
  1  0  0  7  7  4  14  0  0      正解
  0  1  1  7  7  4  14  0  0      正解
  1  1  1  7  7  4  14  1  1      正解
  1  1  0  7  7  4  14  1  1      正解
  1  0  1  7  7  4  14  0  0      正解

続いてテストしてみましょう。

TEST
x_li_li =[[0, 1, 0], [0, 0, 1], [0, 0, 0]]
w_li    =[7, 4, 11]
v       =12
 x1 x2 x3 w1 w2 w3   v  z
  0  1  0  7  4 11  12  0
  0  0  1  7  4 11  12  0
  0  0  0  7  4 11  12  0

どうやら合っているようです！

さいごに

大学の講義で取っていたニューロンモデルを実装しただけでしたが、こうやって実際にプログラムで組んでみると、どのような動作をしているのかを数値を打つだけで見られるようになりました。

さすがにニューラルネットワークをゼロから作るのは至難だったので、今回はしませんでしたが、機会があれば書いてみたいです。